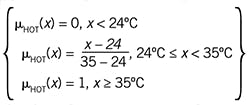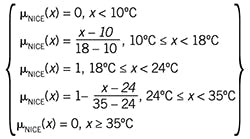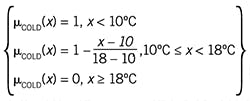Humans can drive a car. They can keep it in a lane, at the right speed, avoid obstacles, obey traffic signals, adjust heaters, switch wipers on and off, and monitor the display. Humans can cook on a grill, or run to a position in left field to catch a fly ball. Humans don't have mathematical models to perform such functions. Instead, they do the analysis and control action intuitively. In the control room, operators interpret and respond to many events—again, without mathematical models.
It would be nice to automate many of those routine and intuitively executed monitoring and control activities. And we can, using several forms of artificial intelligence (AI). This article will describe one approach originally labeled fuzzy logic (FL), but now often called linguistic rules, natural language processing (NLP) or any of many alternate names that don't sound like faulty logic or uncertain reasoning. In 1965, FL was originally introduced by Lofti Zadeh (1921-2017), and to his mathematician and computer scientist community, there was no undesirable connotations to the name. To make it palatable for those in the process industry, I’ll use the term NLP control (NLPC).
Part 2 of this article reveals how NLP is applied for closed-loop control applications.
NLPC is similar to using “if-then” statements in automation. For example, “If the discharge receiver is full, then switch to the other tank.” However, such logical moves abruptly switch from one condition to another. The switch could be disruptive. Smooth transitions are desirable. When stopping a car, we progressively increase breaking force, then progressively lighten up when approaching the stopping point. We don't instantly switch brakes to full on, then full off. NLPC also permits the automation of smooth transitions.
NLPC also permits the automation of qualitative human reasoning. For instance, an automobile operator may look at a car's speedometer and think the speed is a bit slow, and press on the accelerator pedal a bit harder. Or, if climbing a hill and pulling a trailer, the same speed error would be fixed by a medium-large pedal change. The human operator is an effective nonlinear controller, and NLPC can implement human qualitative assessment, such as “a bit slower,” “a bit harder” or “a medium-large change.” Humans give such imprecise instructions to each other, which are fully implementable by the listener. Qualitative assessments and direction are legitimate in control.
NLPC has demonstrated success in control related to chemical and mineral processes, robotics, electronic devices, optimization procedures, home appliances, credit approval, cement-kiln control, anti-lock braking, elevator scheduling, camera auto-focus and many other applications. It also offers many application benefits to the chemical process industry, where human judgements can be routinized. Many control system vendors offer a NLPC product. The author has personally contributed to implementation of NLPC on commercial and lab-scale, inline pH control, correction of weekly plant mass flow measurements from plant-wide material balances, adjusting feed to eight parallel full-scale reactors based on temperature observation, adjusting lab-scale dynamic process model coefficients in real-time and others.
This article presents the basic concepts, terminology, and the relatively simple mathematics of NLP and NLPC with the intent that the reader will be able to determine when and how to use NLP for process analysis and NLPC for decision automation.
Crisp and soft categorization
The engineering and scientific mindset has been programmed to value precise numerical values and crisp logic. However, the same scientists and engineers make personal, life-important decisions every minute with qualitative perceptions and decision analysis. Examples include: when should I leave here to arrive there on time? How should I act when an employee comes in late again? Should I stop or go through that light that just turned yellow?
Although NLP is a more realistic representation of the human view of the world than crisp logic, we're trained to think that Venn diagrams and associated crisp logic are the right way of describing the universe. The crisp logic concepts represent idealizations. They simplify analysis, but don't always represent the real world. To understand and utilize NLP, one must accept two concepts. One is the utility of qualitative assessment and decision, and the second is the pretense of crisp logic.
We act on qualitative understanding, and I’ll use the following as an example in developing NLPC: one might observe that the outdoor temperature is very cold, but the wind is calm, and the sun is shining, and the activity plan for the day doesn't include much outdoor time; and conclude, “Wear a light jacket.” The linguistic terms “very cold,” “calm,” “shining” and “much” are fully adequate descriptors of the set of variables “temperature,” “wind speed,” “sun intensity” and “time duration” needed to make a decision: “light jacket.”
NLP is a system for mathematical manipulation of such qualitative linguistic concepts. When one accepts that qualitative perceptions and assessments are a valid and sufficient basis for good decisions, one is accepting the utility of qualitative assessment.
Second, the pretense associated with precise quantification and calculations needs to be recognized. Yes, we want our chemical processes and automation decisions to be precise, accurate, exact and scientifically grounded. Our enterprise success, our safety record, our employment, and our welfare depend on it. But what data is precise? Is it orifice-measured flow rate, which could have a 2-5% noise amplitude related to fluid turbulence and 5-10% bias related to calibration and the ideal-square-root assumption? Measurement devices are originally selected for “adequate” accuracy, and then are calibrated to be “good enough.” The first-order-plus-deadtime (FOPDT) models that underlye diverse control structures and tuning are just approximations of reality.
When separate individuals tune a controller for a perceived, good enough performance using individually preferred tuning techniques, do they get the exact same values for gain, integral time and derivative time?
The reality is that we let the control computers use uncertain numerical values, imprecise equation coefficient values, and approximate models to perform automation decisions. In this view, they use wrong equations and noise-confounded data to take control actions. Accepting this reality about precision removes a barrier to accepting NLP.
Some definitions are important: process variables are those that describe the process situation or state. For process control these would be measurements (e.g. temperature, pressure, flow rate) or state or quality estimates from measurements (e.g. composition, molecular weight variance). In the example, analysis of the outdoor weather to determine what to wear, these process variables were temperature, wind speed, sun intensity and time duration. From the controller perspective, the process variables are the input variables for the decision procedure.
Conventionally, the term linguistic category is the term chosen to describe the process variables. Above, these were the adjectives and superlatives very cold, calm, shining and much.
Linguistic category membership
Venn diagrams are an idealization that represents the universe of all objects as a rectangle. Within the universe rectangle is a circle that encloses the set of all objects in a particular category.
Consider an application that segregates apples from the universe of objects. Apples are inside the circle. Then take one bite from the apple. Is it still an apple? Or is it totally not an apple? Take more bites, until it becomes an apple core, which is not an apple. At what bite did it move from the is-apple category to the not-apple category? Ask someone who is eating an apple after the second bite, “What are you doing?” Will they answer, “I’m eating a not-apple”? The idealization of either being in the circle or out of the circle is fundamentally incorrect. At every bite there is a belongingness to the linguistic category of apple, and the belongingness fades from unity to zero with each bite.
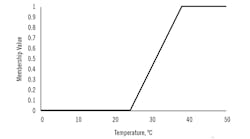
NLP starts with a new definition of belongingness, illustrated in Figure 1, as the classification of outdoor temperature within the linguistic category of “Hot.”
The horizontal axis of Figure 1 presents a range of outdoor temperatures, and the vertical axis, the belongingness of that temperature to the linguistic category “Hot,” meaning an uncomfortable temperature. The curve represents my interpretation of whether a particular outdoor temperature is hot or not. I think any value above 35 °C (95 °F) is uncomfortably hot, and any value below 24 °C (75 °F) is not uncomfortably hot. However, in between, it could be some of either, depending on my activity, the sun, wind or humidity.
The variable represented on the horizontal axis in Figure 1 is the outside temperature, termed the process variable. The linguistic category "Hot" is the human description of the level of the variable. The belongingness of the process variable to the linguistic category is represented on the vertical axis on a 0 to 1 basis. And the membership function is the “curve” on the figure that maps process variable to belongingness. This simple membership function is composed of three straight lines with break points at the process variable values of 24 °C (75 °F) and 35 °C (95 °F), which I defined as definitely in and definitely out of the linguistic category "Hot."
This curve seems to generally agree with my audiences. When I ask how many think 27 °C (80 °F) is hot, about 25% raise their hands. About 75% raise their hands when asked is 32 °C (90 °F) hot. But it seems very likely that those from hotter or colder climates would shift the curve to the left or right. The break points on the membership function reflect human opinion, which could be determined by any criterion that's relevant to the application. For instance, individuals who live nearer to the Equator might say that 30 °C (85 °F) is comfortable, while others who live near the Arctic Circle might perceive the same temperature of 30 °C (85 °F) as uncomfortably hot.
Here are some approaches to determining break points:
- The fraction of people in agreement,
- Opinion of one person,
- Probability of acceptance or un-detection,
- The boss’s opinion,
- Fraction of capacity,
- Fraction of sufficiency, function, perfection or utility.
The people handling the situation that you're considering for an NLP implementation have already thought about the right way to categorize the process variable into linguistic categories. They can state reasonable values for the linguistic categories and associated breakpoints that are appropriate to the application.
Membership functions have numerical values, as illustrated in Figure 1, which can easily be calculated from the equation set below which represents the three line segments:
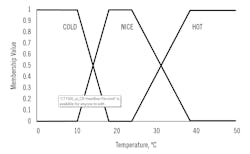
Outdoor temperature can be labeled by other linguistic categories, and Figure 2 represents the use of three: Cold, Nice, and Hot. The two equation sets that follow show how to calculate the respective membership function values:
Figure 2: Three overlapping membership functions expressing the outdoor temperature.
There are several notable features in Figure 2. The membership function for the linguistic category “Nice” has four breakpoints and a trapezoidal central shape. In this description, the membership function is not symmetric.
As is commonly practiced, each membership function has a range of 0 to 1 and some overlap with the membership function of its adjacent linguistic categories. And the breakpoints are common to adjacent membership functions. For example, a temperature of 32 °C (89 °F) has about 0.4 belongingness to the linguistic category “Nice” and 0.6 to “Hot.”
Belongingness is a term used to interpret the meaning of the membership function value. A value of zero indicates that the process variable is definitely not in that linguistic category. A value of unity indicates that it's perfectly, exclusively, in that linguistic category. In-between values indicate the extent that it belongs to that linguistic category.
Because of the linear transition between breakpoints and the common break point locations, as illustrated in Figure 2, at any process variable value, the sum of all membership function values is unity. (Of the other ways to represent membership functions, I like this simple approach.)
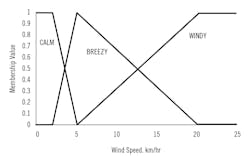
Figure 3: Overlapping membership functions can be asymmetric, such as these describing wind speed.
Outdoor temperature is one process variable used to determine what clothes to wear. This introduction to NLPC concepts will end with control action—choice of clothing. However, wind speed is another process variable that influences choice of clothing, so it needs to be assessed. Figure 3 presents membership functions for three linguistic categories for wind speed. The three equation sets that follow show the mathematical relationships:
Some notable features are that membership functions don't have to be symmetric, and that the middle one can be triangular, not trapezoidal. The graph illustrates that a wind speed of 7 km/hr has a 0.1 belongingness to the linguistic category “Windy,” a 0.9 belongingness to “Breezy” and 0.0 belongingness to “Calm.” Again, because of the linear transition between breakpoints and the common break point locations, at any process variable value, the sum of all membership function values is unity.
In these examples, each process variable only had three linguistic categories. One could extend the temperature descriptions to “Very Cold” and “Frigid,” or to any number of intermediate categories. If there are many distinct linguistic categories in common use by the people that are analyzing and deciding about a process, this indicates that the categories are individually important, and should be included in an NLP description. However, only those descriptions that have distinctly different implications for the human analysis should be used.
Part 2 of this article reveals how NLP is applied for closed-loop control applications.