Though open-channel flow measurement is becoming more important as fresh water is increasingly scarce, most industrial flow measurement is done in closed pipes. Coriolis, ultrasonic, magnetic, turbine and other flowmeters measure flow velocity and flowrate, including volumetric and mass flow, in pressurized, closed pipes. Each flowmeter type has a different operating principle that excels at specific applications.
While not all pipes are round, circular pipes are preferred for most flow applications. Circular pipes allow more uniform flows than square or rectangular pipes, minimizing turbulence and pressure loss. They’re also more cost-effective to manufacture and can be easily connected using standard fittings and joints, simplifying installation.
Get your subscription to Control's tri-weekly newsletter.
There are many good reasons to use round pipes to transport gas, water, petroleum liquids and steam. However, there’s still one issue that no one has figured out: providing a rational value for circular area. Engineers rely on mathematicians to provide formulas for measuring flow velocity and flowrate, and they use π in the calculation. The value of π is the ratio of the length of the circumference of a circle to its diameter.
Finding the area of a circle is a problem that goes back to the ancient Greeks. Around 250 B.C., Archimedes tried to solve this problem by inscribing progressively more polygons inside a circle. The area of each polygon was less than the circle, but as the sides increased, the area of the polygon more closely approximated the circle. He also circumscribed an increasing number of polygons outside the circle. The area of each circumscribed polygon was greater than the area of the circle, but as the circumscribed circles increased, the total area of the polygons came closer to matching the circle. Using a polygon with 96 sides, he concluded that the value of π was as follows: 3 10/71 < π < 3 1/7.
Mathematicians have studied this problem for more than 2,000 years and have computed π to trillions of digits using supercomputers. However, the digits don’t repeat, and π remains a stubbornly irrational number. Today, many people use the values 3.14 or 22/7 as close approximations to the value of π for computing purposes.
There’s no escaping the need to measure the area of a pipe when calculating flow. The formula for measuring volumetric flow is:
Q = A * v
Here, Q is the volume of flow that passes a specific point in a unit of time, A is the cross-sectional area of the inside of the pipe, and v is the average flow velocity. Circular area is calculated using the formula:
Area = π * r2
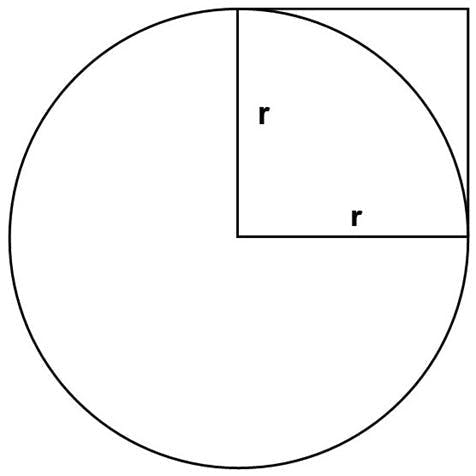
The following figure shows why to use π in calculating the area of a circle:
The area of the square with four sides each equaling r is obviously less than the area of a circle, whose radius is r. The formula requires that some number of squares fit into the circle with radius r. Yet, just as you can’t fit a square peg into a round hole, no definite number of squares will fit into that circular area. The only number that works in this formula is π, which is an irrational, nonrepeating decimal.
The Rope Experiment compares the computed value of the length of the circumference of a circle with the computed value of that length when it’s a straight line. The formula for the circumference C of a circle is:
C = 2 * π * r
Suppose that the circumference of the circle is made up of a rope or string in the shape of a circle. Suppose further that the radius of the circle is 1 inch. Then, the circumference of the circle will be:
C = 2 * π * 1
which equals 2 * π. Omitting the multiplier sign, we can write this more simply as 2 π.
Suppose we take that rope or string and stretch it out to form a straight line. The length of the rope doesn’t change when we make it into a straight line. Only its shape has changed. When we measure the length of this rope as a straight line, there’s no need to bring π into the equation. Instead, using a ruler, we can determine its length as a rational value, such as 6.28 inches. We only need π when measuring circular or curved areas.
While using 3.14 or 22/7 as an approximation for π may work for practical calculations of flow measurement in round pipes, there may be a flaw in the underlying mathematics. Using squares as a unit for measuring circular area yields indefinite results. Saying that a rope changes length depending on its shape is simply a contradiction. After living with π for several thousand years, it’s useful to reexamine our mathematics for measuring circular and curved areas, including the mathematics for measuring flow in round pipes.