The pitfalls and promise of override strategies

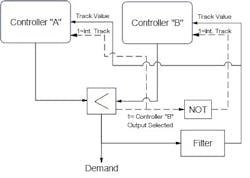
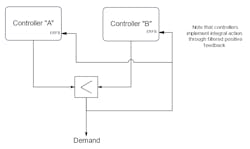
An override control strategy employs two or more controllers in a configuration that allows one controller to act to maintain or regulate one process variable (the main controller) while another controller monitors a different process variable (the constraint variable) to intervene through a high or low signal selector if the constraint is exceeded. While the strategy is a simple one in principle, without adding or configuring features that prevent integral windup and avoid latency in override action, the strategy will not perform well.

When a conventional PID algorithm is used in the implementation of the strategy, integral tracking (or its equivalent) is employed to ensure that there is no integral wind-up in the non-selected controller and that it can intervene without latency when the constraint is approached or exceeded. An alternative implementation of the override strategy, made possible when filtered positive feedback is adopted to provide integral action at the controller, simplifies the implementation, and without additional provisions, provides preemptive action.

This article discusses the importance of adding a first order filter in the integral tracking signal when conventional PID is used in an override strategy and offers evidence of the benefit of using PID algorithms employing positive feedback for integral action.

Override strategy: Conventional PID with integral tracking

Figure 1 illustrates an override strategy using conventional PID algorithms. For the controller that is not selected, the PID integral term follows the track value. The controller output is the track value plus (typically) the controller gain times error. Unless the control error is zero, the PID output is the track value with the error dependent offset applied.

Figure 1: Override strategy implementing integral tracking

When integral tracking is implemented without a filter added to the tracking signal, when the controller actuating error on both controllers is of a sign to drive the output away from the limit, for example, for a low signal selector, when both controllers are acting to reduce valve position, the response can be surprising with adverse consequences. In many applications, this condition may not commonly occur, however the possibility of it occurring cannot be discounted and for this reason a filter should always be added.

In the following discussions, the example used is that of a flow controller acting to modulate the speed of a pump drawing a commodity from a supply tank with an override controller acting on low tank level. In this application it would be a common occurrence for the flow to be higher than setpoint at least transiently while the tank level is low, both conditions demanding a reduction in pump speed. While the conditions may be momentary, when they do occur, without a filter in the tracking signal, the speed demand can be driven to zero in just several controller scans with potentially adverse consequences on plant operation.

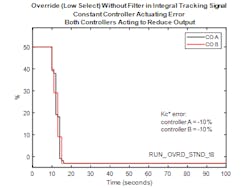
Figure 2 illustrates the behavior of the controllers in an override strategy without a filter in the tracking signal when sustained errors on both controllers are acting to reduce the demand. For clarity the output of the low select is omitted. In this case, the controller execution interval is one second.

Control Parameters:

Controller “A”

Kc=2

Ti=10 sec

Controller “B”

Kc=5

Ti=100 sec

Figure 2: Low-select override strategy with integral tracking without filter

As illustrated in Figure 2 (and Figure 3 in more detail) the output of each controller reduces in alternate scans by the amount Kc*error, this results in the output reaching the low limit in just five scans (five seconds in this case). With higher scan rates, as might be the case in a PLC implementation, the same change in output could occur in less than a second.

Referring to Figure 3, at instant “a” controller output “A” is less than that for controller “B” and is selected as the output at the low signal selector.

In the next scan (instant “b”), controller “A” is registered as being selected since the low selector output and status is that from the previous scan, and controller “B” is switched to the tracking mode. The output of controller “B” is calculated as the last output of the low select minus 10% and that for controller “A” calculated as its last output plus the incremental change (negative) due to integral action. At instant “b” controller output “B” is less than that for controller “A” and is selected as the output at the low signal selector.

In the next scan (instant “c”), controller “B” is registered as being selected since the low selector output and status is that from the previous scan, and controller “A” is switched to the tracking mode. The output of controller “A” is calculated as the last output of the low select minus 10% and that for controller “B” calculated as its last output plus the incremental change (negative) due to integral action. Note that since the IAT for controller “B” is longer than that for controller “A”, the incremental change at the output of controller “B” due to integral action is smaller than that for controller “A” in the previous scan. At instant “c” controller output “A” is less than that for controller “B” and is selected as the output at the low signal selector.

Figure 3: Low-select override strategy with integral tracking without filter (detail)

The cycle repeats while the controller actuating errors remain unchanged until the output reaches the low limit (in this case).

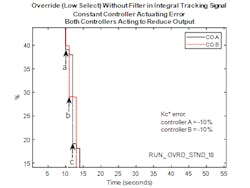
When a filter is applied to the tracking signal, conventional PID with integral tracking performs well in an override strategy but there are some subtleties in behavior that should be considered when the actuating error on both controllers drive the outputs in the same direction to lower the output in the case of a Low select or to raise the output in the case of a High select. Referring to Figure 4, even with a filter applied to the tracking signal, the selected output can still be subject to discontinuity when Kc*error is less in magnitude on the “fast” controller (controller “A”) than it is on the slower controller (controller “B”).

At instant “a”, for one scan, the output of controller “A” is just less than that for controller “B”, and until the next scan, is selected as the output of the low select. In the next scan, the low selector status indicates that controller “A” is selected and controller “B” output is calculated as the filter output minus 10%. Note that at this instant, the filter output is 2% higher than the output of controller “A” so that there is an 8% step in the low select output.

Between instants “a” and “b”, controller “B” output gradually reduces at the rate determined by the controller’s IAT and magnitude Kc*error (-10% in this case). Over the same interval the output of controller “A” (in tracking mode) follows the filter output minus 2% (Kc*error for controller “A”). Note that since the filter time constant is less than the IAT for controller “B”, the controller outputs are converging.

At instant “b”, for one scan, the output of controller “A” is just less than that for controller “B”, to result in the cycle repeating.

Figure 4: Low-select override strategy with integral tracking with filter

The reader is reminded that the behavior described applies when the error is sustained and that in practice, when the controllers are acting to reduce error, the discontinuity in action would not be so repetitive or so great. So saying, in the closed loop example that follows, the possibility of discontinuous

action when both controllers are acting to reduce output for a low select implementation or increase output for a high select implementation, cannot by discounted.

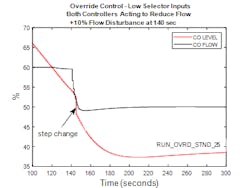
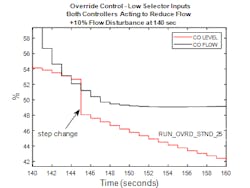
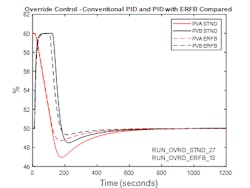
Figure 5 shows the closed loop response for the override strategy when there is an initial imbalance between tank inflow and outflow and a subsequent disturbance in tank outflow that results in the flow controller and level (override) controller both acting momentarily to reduce pump speed. Figure 6 shows the results from the same simulation but for the range 140 to 160 seconds. The conditions may seem contrived but none the less can occur in practice and serve to show the closed loop behavior of a conventional override strategy in this situation. Note that the recommended filter is included in the integral track signal.

Figure 5: Closed-loop response for override strategy with integral tracking with filter

In this example, tank inlet flow is 50% and the setpoint for outlet flow 60%. As a consequence, the tank level (not shown) continuously falls until it reaches the low-level override setpoint (50%) at approximately 120 seconds. At this point, the level controller output is selected so reducing the VFD demand and tank outflow. At 140 seconds, a positive disturbance in pump flow is introduced, in this case reducing the offset between the non-selected flow controller and level controller.

Referring to Figure 6, at approximately 146 seconds the flow controller output is less than the level controller output and is selected by the low select. This situation lasts no longer than one scan since in the next scan the level controller matches the flow controller with a negative offset applied so that the level controller output is reselected at the low select. This results in a step in the VFD speed demand which may not be that consequential unless there is derivative action on error but is nonetheless undesirable. Note that with the filter in the tracking signal, there are no successive step changes in the VFD demand.

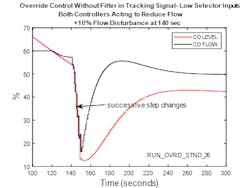
When in an override strategy, integral tracking is implemented without a filter, for the conditions described in the previous case, the successive handing off from one controller to the other results in a series of steps in the output of the low select until the level output is consistently lower than the output of the flow controller when the flow controller offset is positive. This is illustrated in Figure 7

Figure 6: Closer look at closed loop response for override strategy with integral tracking with filter

Override strategy: PID implemented using filtered positive feedback for integral action.

A technique applied out of necessity in pneumatic controllers to obtain integral action is equivalent to using positive feedback through a first-order filter. F.G. Shinskey (internationally known as Greg Shinskey) recognized that there were benefits in applying this method of obtaining integral action in closed loop control. Among the benefits (too many to cover in this article), this method provides the opportunity to implement external-reset feedback (ERF) which can be used to advantage in an override strategy. Note that this method of obtaining integral action and the application of ERF is not universally supported by the vendors of contemporary systems but merits wide support.

When an override strategy is implemented with controllers employing filtered positive feedback for integral action (Figure 8), the implementation is simpler from a user point of view and does not suffer from the discontinuity in action when both controllers are acting to reduce demand (for a low select) or both acting to increase demand for a high select. It is beyond the scope of this article to describe the implementation of PID using filtered positive feedback and the reader is encouraged to explore the references provided at the end of this article for further information on the subject.

When an override strategy is implemented using conventional controllers with integral tracking, the discontinuity on transferring from the output of one controller to the other when both controllers are acting to reduce demand (for a low select) is due to the gain*error at the non-selected controller being less in magnitude than that at the selected controller before the transition occurs.

Figure 7: Closed-loop response for override strategy with integral tracking without filter

When an override strategy is implemented using controllers employing filtered positive feedback configured to use the output of the signal selector as the feedback signal (external reset feedback), in all circumstances, when a controller output is newly selected, there is no change in the output of the non-selected controller other than that determined by the incremental change in the feedback filter output or controller error. As a result, in all circumstances, the transition from one controller to the other occurs smoothly.

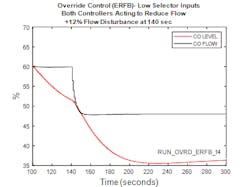
Figure 9 illustrates the closed loop response for the override strategy using external reset feedback. Absent in Figure 9 is the discontinuity evident in Figure 5 which illustrates the closed loop response when the override strategy is implemented using conventional PID controllers with integral tracking. Note that the conditions modelled in Figure 9 and Figure 5 are the same except for a slight increase in the flow disturbance in the case of the external reset feedback implementation, made to ensure that the flow and level controllers momentarily act in the same direction to confirm that there is no discontinuity in action during this condition.

Figure 8: Override strategy implemented with PID controllers employing external reset feedback for integral action

Figure 10 illustrates the closed loop response for a change in flow setpoint occurring at 10 seconds but without the subsequent disturbance in flow introduced in the previously discussed cases. It is evident in this case that for an implementation employing ERFB, the level controller acts in advance of that for an implementation employing conventional PID controllers with integral tracking and that undershoot of the level is less with ERFB. For the implementation employing conventional PID controllers with integral tracking, the filter time constant is set (by conventional wisdom) to match the integral action time of the fastest loop in the override strategy, in this case the flow controller. As a result, while the demand is determined by the flow controller, the filter output closely follows the output of the low select until the level controller PV is close to or slightly lower than the override setpoint. When the override strategy adopts PID controllers with ERFB, the filter time constant on the level controller is the integral action time for the level controller and is longer than that for the flow controller. In this case as the demand is initially increasing under the action of the flow controller, the output of the feedback filter is further behind and lower than the output of the level controller so that the level controller output matches the flow controller output at a higher tank level than in the case of an implementation employing conventional PID controllers with integral tracking. ERFB in this application can be viewed as providing advance action for rapid changes in load to result in better constraint control.

Figure 9: Closed-loop response for override strategy implementing external reset feedback for integral action

The response for conventional PID can be modified to match that of PID controller employing ERFB but only by increasing the complexity. For the strategy implementing conventional PID, using the state of the signal selector, when the flow controller output is selected, the filter time constant can be set to match the integral action time of the level controller (controller A), and when the level controller output is selected, the filter time constant can be set to match the integral action time of the flow controller. Note that in order to accommodate this, the implementation platform has to allow the filter time constant to be written to by configured logic without disturbance and if this is not the case, the filter would have to be built with the basic function blocks provided.

Future constraint control possibilities

One of the advantages of model predictive control (MPC) in constraint control is the future prediction of a constraint violation enabling proactive action. This capability could be achieved to some degree by the use of a future value prediction for a constraint PV of an override controller. The calculation is used in batch profile control and endpoint prediction besides a full throttle setpoint response. The calculation is rather simple and easily adjusted. A dead time block is used to create an old value of the PV that when subtracted from the new PV and divided by the dead time is the rate of change of the PV. The dead time is chosen to be large enough to provide a good signal to noise ratio. This simple method introduces no dead time into the calculation seen in more traditional methods. The rate of change multiplied by a time interval to give a predicted change in PV that is then added to the new PV to create a future value PV of an override controller to enable a fast proactive reaction to prevent constraint violation. The override controller tuning would be based on the dynamics of the new PV response to the manipulated variable.

Takeaway

Figure 10: Closed-loop response comparison: conventional PID and PID with ERFB

While override strategies can be implemented with conventional PID algorithms utilizing integral tracking to prevent integral wind-up on the non-selected controller(s), without a filter in the tracking signal, unexpected and potentially damaging upsets can occur when more than one controller is called on to reduce demand (for a low select) or increase demand in the case of a high select. When a filter is applied to the integral tracking signal, conventional implementations of PID serve well in override strategies but there remains the potential for a discontinuity in action when more than one controller is asserting influence. Implementing an override strategy using PID algorithms employing filtered positive feedback offers reduced complexity and pre-emptive action with no added logic.