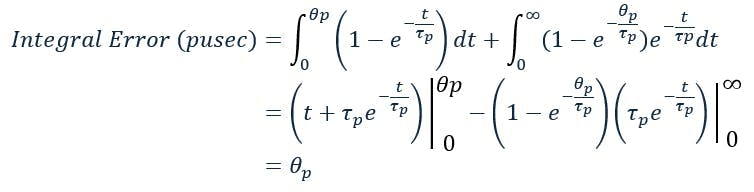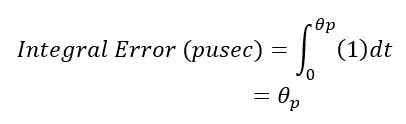Face-off: Smith Predictor vs. deadtime compensated PID

In a previous article by the authors, “Deadtime compensation opportunities and realities,” evidence showed how simple implementation of deadtime compensation improves loop performance over and above what’s achievable with a conventionally implemented proportional-integral-derivative (PID) controller, when it adopts filtered positive feedback and a deadtime is inserted in the feedback signal. This article goes further and challenges the traditional view that the Smith Predictor is the pre-eminent choice for deadtime compensation. It establishes, by analysis, the best theoretical integral absolute error (IAE) for a Smith Predictor exactly modeling the process. Then, it compares the performance of the Smith Predictor and deadtime-compensated controller employing external reset feedback (ERFB).

Get your subscription to Control's tri-weekly newsletter.

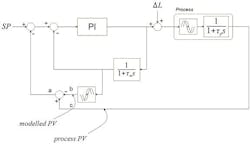
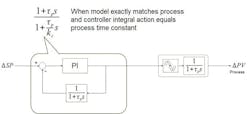
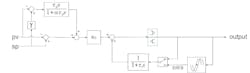
Figure 1 shows the Smith Predictor controlling a self-regulating process with a response characterized by a deadtime followed by a first order lag.

Analysis

Normalized values are assumed, so there’s no requirement to be specific about units of measurement. Normalized values are derived by dividing the physical quantity by a base quantity, which for these studies is a load or setpoint change, so the normalized quantity (lb/hr, psi etc.) per unit (PU) doesn’t have units. For emphasis and to avoid confusion, units for the calculated IAE are expressed as per unit (PU) seconds.

For an unmeasured load disturbance

Referring to Figure 1, when the model and process are exactly matched, a change in controller output equally affects signals “b” and “c,” so there’s no change in signal “a.”  This suggests that, for load changes, the Smith Predictor can be represented by Figure 2, which lends itself to a simple analysis. It should be noted that the load change is inserted at the controller output (input to the process) and not at the PV, which is a common assumption in academic studies, and leads to performance predictions for the Smith Predictor for load changes not achievable in practice. 

In Figure 2, when controller gain is high, the transfer function of the PI controller (with negative feedback inherited from the Smith Predictor as the response of the process without deadtime) reduces to a lead term 1+τ_p to cancel the lag term characterizing the process response to the load change. The net result is a correcting change in controller output matching the load change, but of opposite sign and delayed by the process deadtime. Figure 3—a distillation of Figure 2—illustrates the action of the Smith Predictor for a load change. It should be noted that the performance with high gain, which might not be achievable in practice due to the presence of secondary lags in the process, represents the best theoretical performance. Even if derivative action is added to the controller, the response can’t be improved due to the influence of the feedback local to the controller.

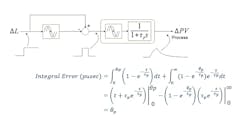
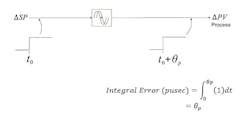
Not surprising, when the integral of the PV disturbance (integral error) is calculated from the exponential expressions for the process response in the interval before corrective action is taken and the interval of recovery when the corrective action is taken, for a PU change in load, the integral error depends directly, and only, on the process deadtime. 

For the Smith Predictor, for a step load disturbance (Figure 3), the integral error is given by:

For a change in setpoint

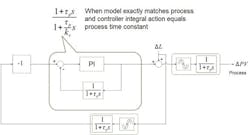
Figure 4 illustrates the equivalent transfer function block diagram for a setpoint change when the model exactly matches the process, and the controller integral action time equals the process time constant. In this case, for high controller gain, the transfer function for a PI controller with the negative feedback inherited from the Smith Predictor reduces to 1+τ_ps, canceling the process lag to leave only the deadtime to determine the PV response for a change in setpoint (Figure 5). It should be noted that, since the output of the Smith Predictor is the controller output (and MV), practically, the response of the lead term (1+τ_pS) to the step change in SP is limited in amplitude and can’t completely cancel the process lag. The effect of the controller output limit on achievable IAE will be illustrated later.

For the Smith Predictor, for a step change in setpoint (Figure 5), the integral error is given by:

Model results—Smith Predictor

To directly compare modeled response with theoretical calculations, the process is first modeled as deadtime (30 sec), followed by a first-order lag (200 sec) and the Smith Predictor implemented as shown in Figure 1. This study also shows and discusses the results for the equivalent second-order system and deadtime, since few systems are adequately represented by a first-order lag plus deadtime. The Series PID form (per ISA 5.9) is adopted and implemented using filtered, positive feedback to replicate the method adopted by a recognized DCS vendor.

Note that the IAE on the plots is reported in units percentage second (%sec) and is the integral of the absolute error (|pv-sp|), which depends on the magnitude of the load or setpoint change. When discussing performance and tabulated comparisons, per unit (PU) IAE helps compare performance. The PU IAE is the reported IAE divided by the magnitude of the load or setpoint change. The dimension of the PU IAE is seconds.

For an unmeasured load disturbance (first order plus deadtime process approximation)

The step disturbance is applied at the controller output, so the manipulated variable first increases by 10%, where it remains until corrected by the controller under the influence of the Smith Predictor.

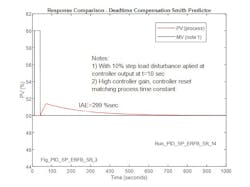
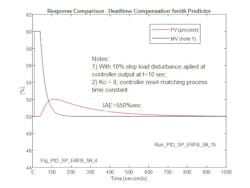
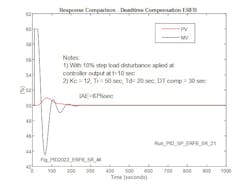
Figure 6 illustrates the response of the Smith Predictor for a 10% increase in load. In this case, the controller gain is high, so that the PU IAE is 29.9 sec (299/10), closely matching the process deadtime (30 sec) and theoretical IAE. When gain is reduced, typically a practical requirement due to the presence of higher order poles in the process, PU IAE increases as shown in Figure 7 to 55 sec (550/10), which is 1.8 times the best achievable value.

For an unmeasured load disturbance (second-order plus deadtime process approximation)

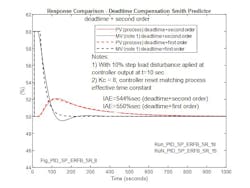
In this case, the process is modeled as a deadtime equivalent to the actual process transport delay and second-order interactive lags to better represent the typical process, for instance, a shell/tube heat exchanger. For equivalence to the deadtime plus first-order lag approximation, for the second-order process model, the actual deadtime is 16 sec and the lags are 160 sec and 25 sec, respectively. Figure 8 illustrates the response for the second-order process, and includes the response for the first-order plus deadtime approximation for comparison. Note that the first-order approximation includes the apparent deadtime assessed in approximating the second-order response, so the total deadtime is larger. Notably, when the Smith Predictor utilizes the deadtime plus first-order lag approximation of the controlled second-order process, the IAE is close to that obtainable when the Smith Predictor model and process exactly match. It’s worth noting that with a second-order process, the theoretical lowest achievable IAE (for a first-order process) can’t be achieved by increasing the gain, and with high gain, low-level oscillation occurs.

For a setpoint change (first order plus deadtime process approximation)

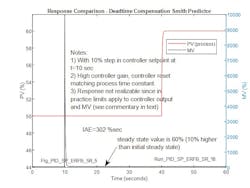
For a setpoint change the theoretical best performance (minimum IAE) is only achievable if the controller output and the MV (for instance the valve) has no limit. This is never the case in practice, but it’s allowed here to demonstrate the alignment between the model results and the theoretical behavior of the Smith Predictor. If this practicality is ignored for the sake of verifying the model behavior, the model predicts that the step in setpoint is followed by a step in PV one process deadtime later, and that the PU IAE is 30.2 sec (302/10), matching (very nearly) the process deadtime. Recognizable in Figure 9 is the proportional plus derivative action characterizing the MV as the leading response to the setpoint change shown in Figure 4.

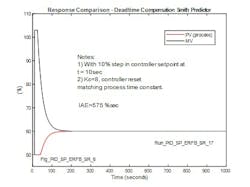
In Figure 10, response for 10% setpoint change with Smith Predictor implemented and the modeled process in the Smith Predictor matching process illustrates the response when the controller output is limited (to 103%) and gain is reduced to a more practical value, in this case 8 (same as the reference case for a load disturbance). The PU IAE increases to 57.5 sec (575/10), which is approximately the same as for the load disturbance.

For setpoint change (second order plus deadtime process approximation)

For the reference second-order process described, the response for the Smith Predictor for a setpoint change is shown in Figure 11. Also included in Figure 11 is the equivalent response for the first-order process. It’s noted that, with the same controller gain for the second-order process, the PV slightly overshoots the setpoint and the IAE is 11% higher. Notable for the second-order process, the gain can be increased beyond values considered reasonable, i.e. to 50 with little improvement in IAE. This is still approximately twice the theoretical limit based on matching, first-order Smith Predictor model and process with high gain and no limit on output.

External reset feedback (ERFB) with deadtime compensation

The alternative, simpler implementation of deadtime compensation using ERFB is shown in Figure 12. It must be noted that the output limits, other than the high and low limit being specified (103% and 0%, respectively), require no additional logic to prevent integral wind-up. This is a benefit of this particular implementation of integral action.

For an unmeasured load disturbance

For an unmeasured load change, Figure 13 shows the response for a controller implementing ERFB with a delay matching the effective process deadtime modifying the feedback signal. To permit a direct comparison of performance with that of the Smith Predictor, results are provided for the same deadtime plus second-order process model adopted for predicting Smith Predictor performance. Without exhaustive tuning for a 10% lead disturbance, the IAE is reduced to less than one-quarter of the lowest achievable with the Smith Predictor (Figure 6) and one-eighth of the IAE achievable with the Smith Predictor implementing a more practical controller gain (Figure 7). The peak change in process variable for the deadtime compensated ERFB implementation is approximately half of that for the Smith Predictor with a practical gain setting (Figure 4). This would further distinguish the ERFB implementation in applications where operating within constraints is critical.

Cases not included here (for brevity) show that even the conventional PI controller without deadtime compensation can outperform the Smith Predictor for an unmeasured load disturbance (Table 1).

Table 1: IAE—unmeasured load disturbance

For a setpoint change

For a setpoint change, it’s important to recognize that, with a large change in setpoint and relatively high controller gain, the controller output typically reaches the output limit, so the improvement in response by adding deadtime compensation, derivative action, or in part or wholly implementing 2 DOF, can’t be easily discerned. For this reason, the setpoint change is restricted to 2% for this study. 

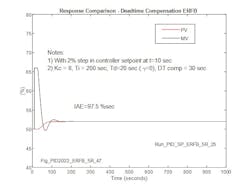
Figure 14 shows the response for a step change in setpoint for a PID with deadtime compensation. In this case, the derivative is acting on the PV only (γ = 0), so there’s no augmentation based on the derivative of the setpoint. There is a 15% improvement in IAE compared to that for the Smith Predictor implementing a practical controller gain. When γ = 1 (derivative on error), IAE is further reduced to 65% of that for the Smith Predictor, and only 25% greater than the theoretical minimum for the Smith Predictor, which is only achievable with an unrealistic high gain requiring an unrestricted controller output. 

Table 2 compares the IAE for each of the regimes noting that for this comparison. The result for the Smith Predictor with practical gain setting is obtained for a 2% change in setpoint and slightly less than for the 10% change previously presented.

Table 2: IAE—setpoint change

Comparing sensitivity to modeled deadtime change

Figure 15 shows a response when modeled deadtime (compensation) is varied by +50% and -50% of the process deadtime for the subject, lag-dominant process. Results for the manipulated variable are shown (rather than PV) because they more clearly show response differences. For the Smith Predictor, the effect on loop stability is less than for the PID controller with deadtime compensation. Notable in this comparison is the trend with DT compensated PID, which indicates the response becomes more oscillatory for any departure (higher or lower) from the deadtime matching the process deadtime. This runs counter to the common opinion that it’s helpful to start with compensating deadtime greater than the process deadtime.

Figure 16 shows the response for a deadtime-dominant process when the modeled deadtime (compensation) is varied +50% and -50% of the process deadtime (in this case 100 seconds). Notable, and aside from the main purpose of this comparison, is the similarity between methods of the IEA and that IAE is close to the theoretical minimum for the Smith Predictor (1,000 %sec or 100 sec PU IAE). This suggests that deadtime-compensated PID offers little performance improvement compared to the Smith Predictor in deadtime dominant applications. However, it does offer the benefit of a simpler implementation with a familiar operator interface. Both strategies are affected by a mismatch between modeled deadtime and process deadtime, with the Smith Predictor soon diverging to be limited in amplitude only by controller output limits.

Conclusions

For a lag-dominant process it’s striking that the minimum achievable PU IAE for an unmeasured load disturbance for the controller implementing the Smith Predictor (by analysis equal to the process deadtime) is significantly greater than the ultimate limit for the IAE for an uncompensated PID controller. For the reference process, this would be approximately 4  sec (ϑ_p²/( ϑ_p+τ_p)). It’s hardly surprising that PID controllers are so widely used in control applications, where the primary (and common) objective is to minimize process variable integral error for unmeasured load disturbances. 

For lag-dominant processes, when controller integral action is implemented using filtered positive feedback to allow deadtime compensation by simply adding a delay to the feedback signal, loop performance for an unmeasured load disturbance is much improved over what’s obtainable with the more complex Smith Predictor. For deadtime-dominant processes, the performance of the deadtime-compensated PID isn’t materially better than for the Smith Predictor. However, since the deadtime-compensated PID is less sensitive to a mismatch between the modelled/compensating deadtime and process deadtime, and the deadtime-compensated PID is simpler to implement, it is still favored for use in deadtime-dominant processes.

Not mentioned so far, for the Smith Predictor, the PV for the PID controller isn’t the process PV except in the steady state. Though the process PV can be displayed and trended by configuring a separate point in the control system database, it would be a departure from the normal practice of relying on the PID block PV indication to access the process condition. That the normal, vendor-provided PID faceplate displays the controller PV can lead to operator error in the case of a Smith Predictor implementation.

For setpoint changes, the Smith Predictor outperforms a deadtime-compensated PI controller, but not a PID controller with deadtime compensation. 

The deadtime-compensated PID controller can outperform the Smith Predictor for setpoint changes and unmeasured load changes. This strongly suggests that implementing the PID controller using integral action through positive feedback should see wider use. This would allow a simple and effective means of deadtime compensation when deadtime is adjusted to match process deadtime to avoid ERFB deadtime that’s smaller or larger than the actual deadtime.