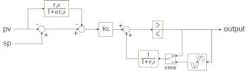
Controller
Process model
For a self-regulating process, the process is modeled as a deadtime followed by a lag. For convenience, the loop gain is assumed to be unity. The load disturbance is inserted between the deadtime and lag, though it could be equally represented as a disturbance applied to the controller output with no change in response except delaying the timing of the change in process variable (PV). In each case, the load disturbance is 10% applied at 10 sec. The practice of applying the disturbance on the PV is often adopted by academics, but has no practical value except to replicate a transmitter failure. It gives a false measure of loop performance with respect to peak change in process variable for an unmeasured load disturbance. For an integrating process, the load is disturbed from the initial steady state (50%) to 60% at 10 seconds.
Self-regulating process—lag dominant
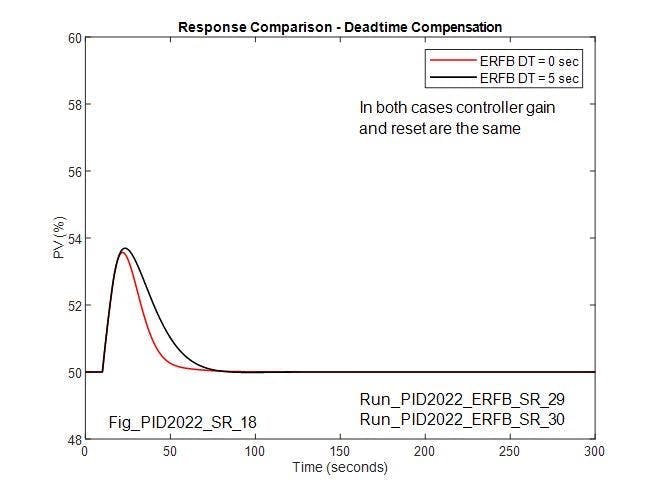
In this case, process deadtime is 5 seconds and process lag is 20 seconds. For the reference case, the controller is tuned for maximum disturbance rejection, which for this lag-dominant process results in a gain of 2 seconds and reset of 15 seconds without overshoot. The reference response is shown in Figure 3, as is the response for the same disturbance when deadtime matching the process deadtime (5 seconds) is included in the ERFB signal. For the reference response, the peak change in PV is 3.7% and the IAE is 7 %sec. When matching deadtime is added in the ERFB signal, the peak change in PV is only slightly different, but the recovery is longer. The IAE increases to 108 %sec. Since the deadtime in the ERFB signal delays the integral action, the increase in the IAE is understandable; however, there’s an opportunity to re-optimize the controller tuning parameters when deadtime is included in the ERFB.
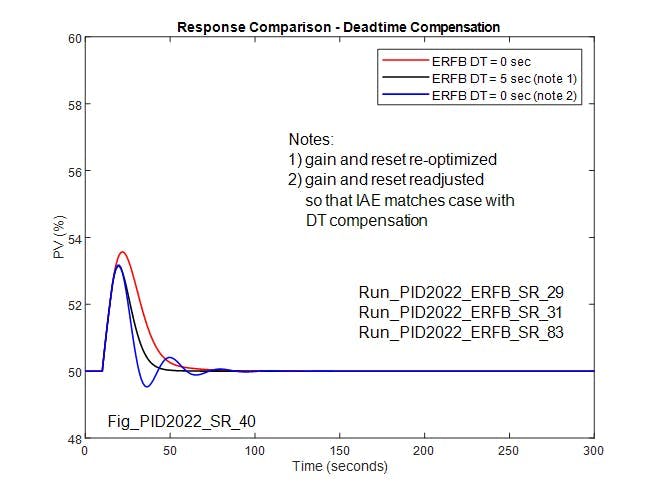
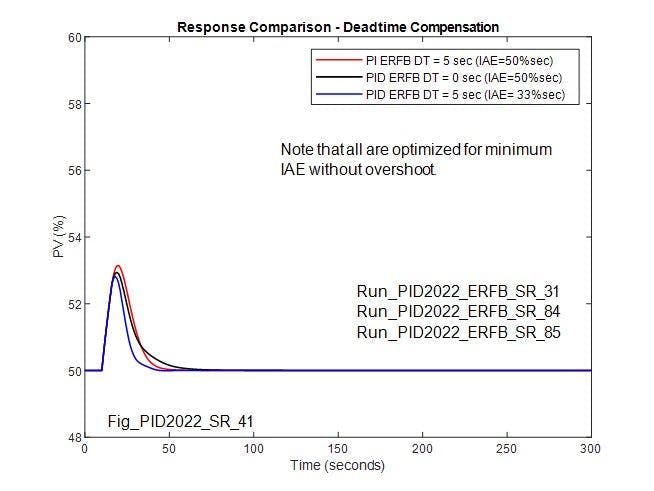
Figure 4 confirms that, with matching deadtime in the ERFB signal, the controller gain and reset can be re-optimized to provide a response for load changes that’s an improvement over what’s obtainable without deadtime in the ERFB signal. With re-optimized control parameters (Kc = 3.7 and Tc = 12 sec), the IAE is 50 %sec, and is significantly lower than what’s obtainable without deadtime in the ERFB. This assertion questions whether the performance of the proportional integral (PI) loop without deadtime compensation can be improved by further adjustment of the PI control parameters, so the IAE matches that of the compensated controller. Figure 4 shows that, while the IAE for the case without deadtime compensation can be reduced to match the case with deadtime compensation, the response obtained is underdamped, and depending on the application and loop interaction, may not be acceptable.
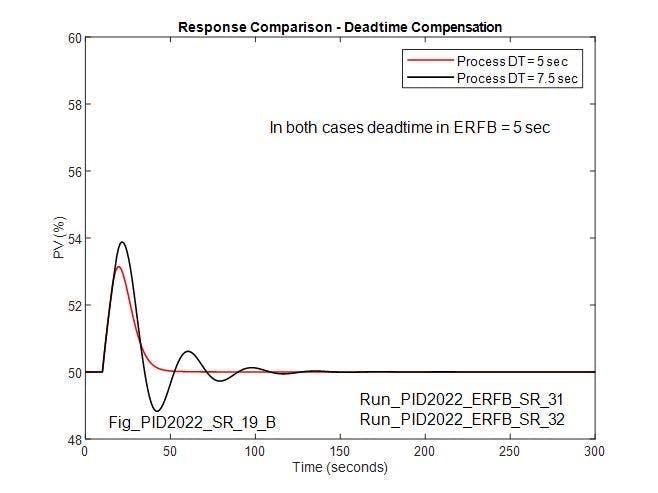
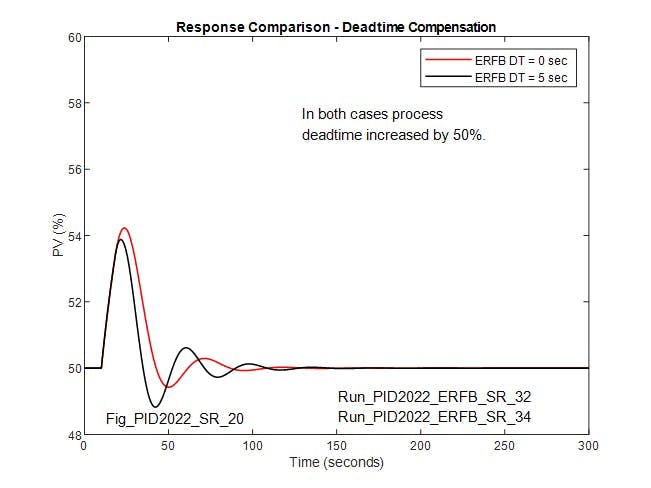
Figure 5 compares the re-optimized response with 5 seconds of process deadtime and matching deadtime in the ERFB, with the response when the process deadtime is increased to 7.5 seconds with the same controller settings. In this case, the loop is oscillatory, not settling for approximately four cycles. The question is whether the effect of an increase in process deadtime is worse when deadtime is included in the ERFB and the controller settings re-optimized than the reference case without deadtime in the ERFB.
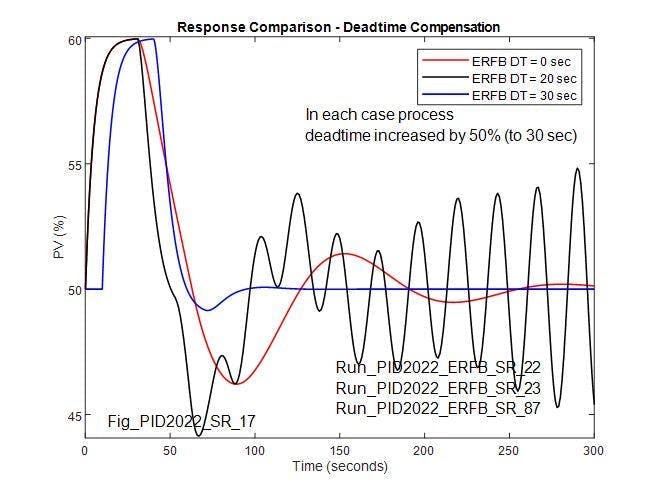
Figure 6 addresses this question, comparing the response of the reference case (when there’s no deadtime in the ERFB) to when 5 seconds deadtime is included in the ERFB and the controller is re-optimized and, in both cases, the process deadtime is increased to 7.5 seconds. While increasing the process deadtime by 50% reduces the damping on both, the effect is greater when deadtime is included in the ERFB for deadtime compensation, and may suggest adapting the ERFB deadtime.
Stability margin equal performance—gain
Stability margin equal performance—process deadtime variation
Adding derivative action—lag-dominant process
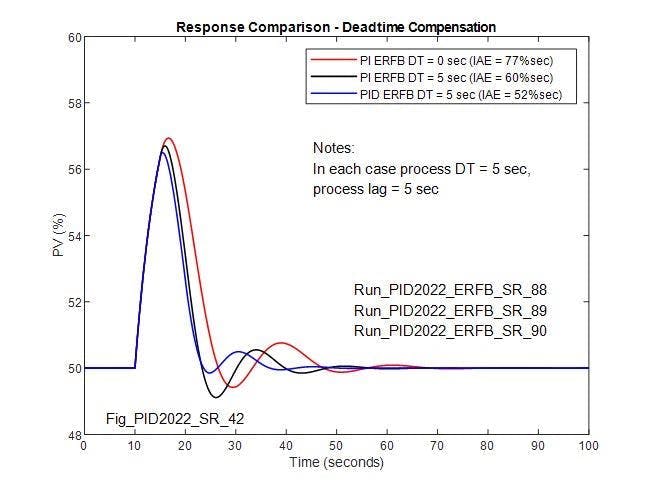
For a lag-dominant process, when derivative action is added without deadtime compensation, the performance of the deadtime-compensated PI controller can be matched by an optimized PID controller, and can be further improved by adding deadtime compensation to the PID controller to reduce the IAE by 56% of that for the uncompensated PI controller(Figure 9). Derivative action, often overlooked or intentionally avoided due to a reputation gained through improper implementation, should be considered the first of several options for improving loop performance.
Self-regulating process—deadtime dominant
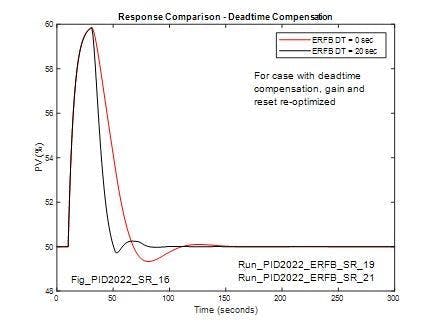
Figure 11 confirms it with matching deadtime in the ERFB signal. The controller gain and reset can be re-optimized to provide a response for load changes that’s an improvement over what’s obtainable without deadtime in the ERFB signal. With re-optimized control parameters (Kc=1.1 and Tc=5sec), the IAE is 240 %sec and is significantly lower than what’s obtainable without deadtime in the ERFB.
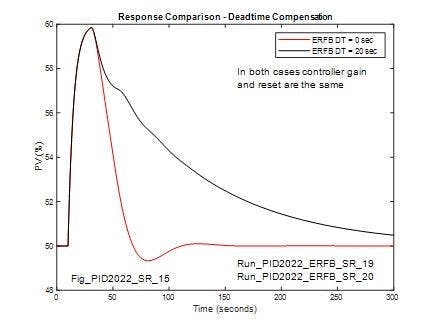
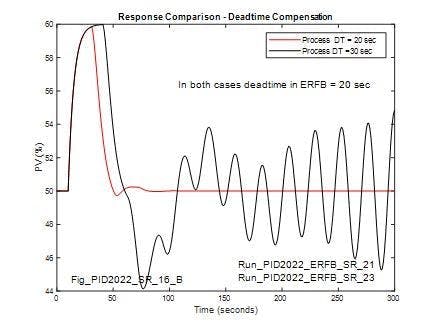
When the compensating deadtime in the ERFB matches the process deadtime and the controller tuning parameters are optimized, the loop performs better than without deadtime compensation. However, as shown Figure 12, this improved performance can’t be achieved without reducing robustness. Figure 12 compares the re-optimized response with 20 seconds process deadtime and matching deadtime in the ERFB to the response when the process deadtime is increased to 30 seconds with the same controller settings. In this latter case, the loop is unstable and the amplitude diverges with time.
Adding derivative action (deadtime-dominant process)
Integrating process
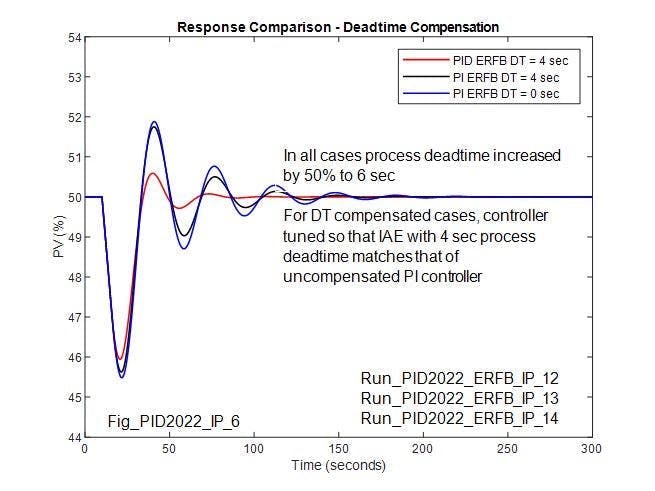
Figure 16 compares response for process gain and deadtime variation. Interestingly, for a 50% increase in process gain, the response for the uncompensated PI and compensated PI are more oscillatory, but not greatly different from each other, and could be stabilized by a complimentary adaptive change in controller gain. For a 50% increase in process deadtime, the response for the compensated PI controller is more oscillatory than for the uncompensated controller. As with the self-regulating process, when the deadtime in the ERFB is increased to match the process deadtime, there’s a marked improvement in the response, which is notably better than for the uncompensated controller. As with a self-regulating process, this suggests that adjusting just one parameter at the compensated controller (ERFB deadtime)can achieve loop stability, while controller gain and reset with the uncompensated controller would require adjustment.
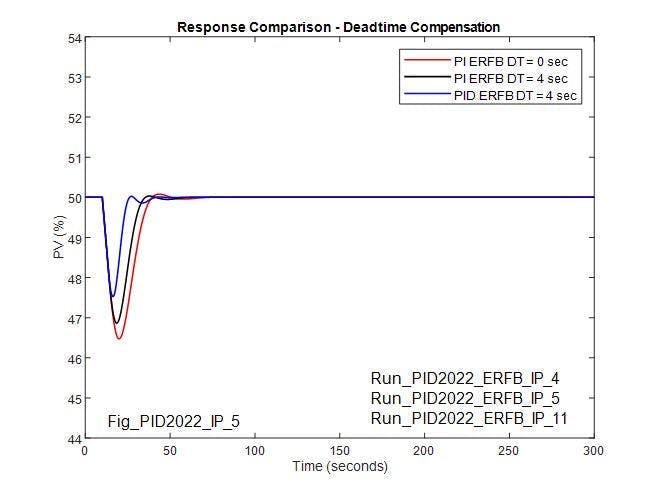
While a change in process deadtime reduces the stability of the optimized controller, the reduction in stability is less when the controller is tuned for equal performance to the uncompensated PI controller without a matching change in the compensating deadtime. In each case, the compensated controller is tuned, so IAE matches the uncompensated PI controller. For an unaccountable change in process deadtime, the compensated controller with derivative action added provides better (more stable) response when the controller is tuned, so IAE matches the uncompensated PI controller with the original deadtime of 4 seconds. For the compensated PI controller, stability is only slightly better than for the uncompensated PI controller when there’s an unaccounted change in process deadtime.